Résumé congruences

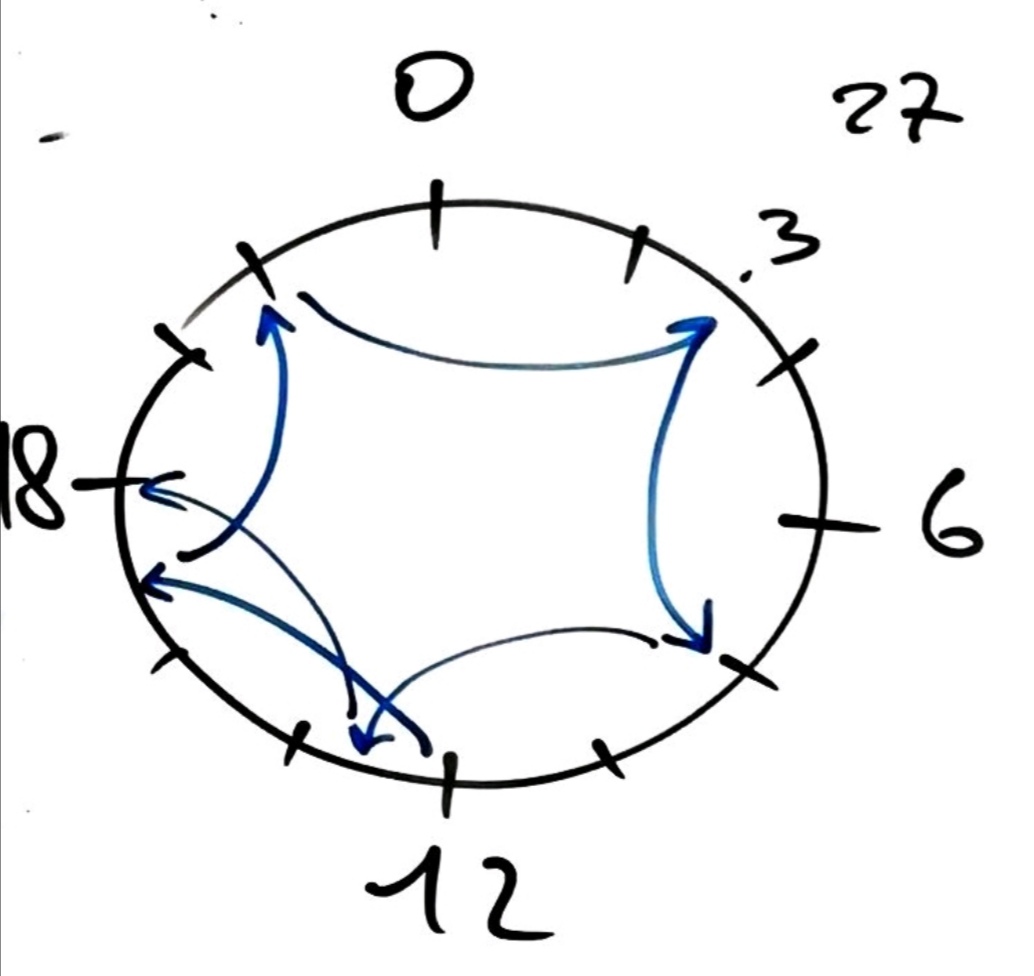
Définition

$a \equiv b [n]$ se dit «a est congru à b modulo n». Cela signifie (équivalences):

a et b ont le même reste dans la division euclidienne par n.
a et b se retrouvent au même endroit sur l’horloge.
il existe un entier relatif k tel que $b = a + kn$ , autrement dit $b - a = kn$ ou même $a - b = kn$ si on prend pour nouveau k l’opposé de k.
$a - b$ est un multiple de n

Sans retenue, le travail sur les octets se fait modulo 256.

$a \equiv b \Leftrightarrow b \equiv a$
$a \equiv b \land b \equiv c \Rightarrow a \equiv c$
formules de compatibilité en supposant les primes congrues:
- $a + b \equiv a^{'} + b^{'}$
- $a - b \equiv a^{'} - b^{'}$
- $a \times b \equiv a^{'} \times b^{'}$
- $a ˆ k \equiv a^{'} ˆ k$ mais $2ˆ4 \nonequiv 2ˆ1 [3]$

Pour savoir si 12 et 166 sont congrus modulo 7:

Première méthode:

12 = 7×1+5

166 = 140 + 26 = 140 + 21 + 5 = 7× (20+3) + 5

Donc $12 \equiv 166 [7]$ car ils ont le même reste dans la DE par 7.

Deuxième méthode:

166-12 = 154 = 7×22

Donc $12 \equiv 166 [7]$ car leur différence est un multiple de 7.

Le plus petit nombre positif congru à a modulo n est le reste de la division euclidienne de a par n.