Théorie musicale pour les matheux

Pourquoi cette page

Étant retombé par hasard (en fait pas vraiment) sur THE GEOMETRY OF MUSICAL CHORDS, j’ai demandé à un collègue très fort en maths de m’expliquer certains concepts. Réciproquement, j’ai eu à lui expliquer certains concepts musicaux afin d’avancer sereinement dans le papier.

Remarque : on utilisera le plus souvent la notation anglaise car c’est elle qui est utilisée dans le papier.

Modélisation

Simplification timbrale

Concept fondamental pourtant négligé ici : les sons des instruments de la vraie vie ne sont pas sinusoïdaux et cela a tout un tas d’implications concernant la consonance ou la dissonance de deux « notes ». Ici une note sera sans harmonique : une sinusoïde pure, donc totalement définie par une fréquence.

Quotient octavial

On ne peut pas faire plus consonant que deux notes séparées par une octave (fréquence multipliée ou divisée par 2). Les notes séparées par une ou plusieurs octaves portent donc le même nom (fr, en) :

• Do, C
• Ré, D
• Mi, E
• Fa, F
• Sol, G
• La, A
• Si, B

Comme, en quelque sorte, on assimile une note à toutes les notes à une octave près, on travaillera « modulo une octave ».

Pour avoir tout de même un repère, un des La, le La4 a pour fréquence 440Hz.

Des résultats de psycho-acoustique donnent que dans les aigus, l’octave pur n’est pas forcément le plus « juste ».

Discrétisation tempéramentale

Le deuxième intervalle le plus important est quand la fréquence est multipliée par 3. Appelons-ça arbitrairement cet intervalle « I3 » (on verra plus tard que c’est environ une octave + une quinte juste).

Les musiciens veulent une certaine symétrie. Si à partir d’une première note, on joue une deuxième note à l’intervalle I3, on veut pouvoir jouer une troisième note à l’intervalle I3 de la deuxième, etc… Comme aucune puissance de 3 n’est une puissance de 2, aucune chaîne de I3 n’aboutira exactement à la note de départ à une octave près. Différentes solutions d’approximation existent à ce problème, nous choisissons ici le « tempérament égal ».

Comme $(\frac{3}{2}{)}^{12}\approx 129.75\approx 128=2^7$, une octave comportera 12 notes, séparées par un intervalle appelé un « demi-ton » (le ♯ « monte » la note d’un demi-ton, le ♭ « baisse » la note d’un demi-ton) :

A - A♯/B♭ - B - C - C♯/D♭ - D - D♯/E♭ - E - F - F♯/G♭ - G - G♯/A♭ (et retour à A, l’octave de A)

Attention, il y a aussi des E♯, des F♭, des B♯, des C♭, des Fx (double dièse), et des B♭♭ (double bémol). Grâce à l’enharmonie (possibilité de désigner par un autre nom une note d’une même fréquence), on peut confondre ces notes si elles ont la même fréquence mais différents noms.

Il y a une totale symétrie entre les fréquences des notes du tempérament égal. Elles sont définies par les formules (réciproques l’une de l’autre) :

$n=69+12lo{g}_2(f/440)$ $f=440\times 2^{\frac{n-69}{12}}$

Remarque : La note A4 est arbitrairement numérotée 69 (voir la norme MIDI sur WP).

Autres harmoniques

Les considérations de cette section ne sont pas strictement utiles pour la compréhension de The geometry of musical chords mais je n’ai pas d’autre endroit pour en parler.

Supposons qu’un corps musical (une corde, un cuivre…) vibre à sa fréquence propre, que l’on note $f$ (voir WP). En plus du double et du triple de cette fréquence de départ, tous les multiples entiers de cette fréquence correspondent :

• à une harmonique du son de cet instrument car ce son n’est sans doute pas pur ;
• à des intervalles qui correspondront à leur tour à des notes, et c’est ce qui nous intéresse ici.

Nous allons visualiser les liens entre harmoniques et notes sur un axe gradué de 20Hz à 20000Hz, mais avec deux types d’échelles.

Pour commencer, quelles valeurs visualiser ? Partons par exemple du B♭0 ($n=22$ et $f\approx 30\text{Hz}$). La liste des premiers multiples de $f$ est (sans l’unité) :
$2f\approx 60$ ; $3f\approx 90$ ; $4f\approx 120$ ; $5f\approx 150$ ; $6f\approx 180$ ; $7f\approx 210$ ; $8f\approx 240$ ; etc…

Si la fréquence de l’harmonique est de la forme $2^{k}f$, la note correspondante est une octave de B♭0. C’est même B♭$k$. il faut aller jusqu’à B♭9 ($n=130$ et $512f\approx 15360$) pour atteindre le B♭ le plus aigu qu’on puisse entendre (en tout cas les plus jeunes). Voici la liste des fréquences des B♭ (il suffit de doubler pour passer de l’un à l’autre) :
$2^{0}f\approx 30$ ; $2^{1}f\approx 60$ ; $2^{2}f\approx 120$ ; $2^{3}f\approx 240$ ; $2^{4}f\approx 480$ ; $2^{5}f\approx 960$ ; $2^{6}f\approx 1920$ ; $2^{7}f\approx 3840$ ; $2^{8}f\approx 7680$ et $2^{9}f\approx 15360$.

C’est extrêmement étendu. Nous allons de plus zoomer sur la fondamentale et ses premières harmoniques. Disons les 15 premières, de $2f$ à $16f$.

Ma connaissance est limitée à certains instruments, mais on peut supposer que si $f$ est la fréquence de la note la plus grave d’un instrument (disons même la fréquence de sa résonance propre), alors on ne sort raisonnablement pas de note plus aiguë que $16f$. Par exemple la note la plus grave d’un sousaphone ou la corde la plus grave d’une basse est un E1 avec $f\approx 40\text{Hz}$. Cela correspondrait à aller jusqu’à E5 avec $16f\approx 640\text{Hz}$. C’est très aigu pour ces instruments. À partir de B♭0, cela correspondrait à aller jusqu’à B♭4.

Échelle linéaire

Avancer d’une certaine distance vers la droite correspond à l’ajout d’une certaine fréquence. Si l’axe gradué de 20Hz à 20000Hz mesure 20cm, 1cm représentera environ 1000Hz.

• De 20Hz à 1000Hz on aura B♭0, B♭1, B♭2, B♭3, B♭4 et B♭5.
• De 1000Hz à 2000Hz on aura B♭6.
• Rien de 2000Hz à 3000Hz.
• De 3000Hz à 4000Hz on aura B♭7.
• Rien de 4000Hz à 5000Hz, rien de 5000Hz à 6000Hz, rien de 6000Hz à 7000Hz !
• De 7000Hz à 8000Hz on aura B♭8.
• B♭9 sera très isolé aux trois quart du graphique.

Le « zoom de B♭0 à B♭4 » est donc intégralement contenu dans le premier centimètre de l’axe ! La fondamentale B♭0 et ses 15 harmoniques sont espacées de 3 dixièmes de millimètre.

Notre perception des hauteur de sons (mais aussi des volumes sonores) est plus fidèlement représentée avec une échelle logarithmique.

Échelle logarithmique

Avancer d’une certaine distance vers la droite correspond maintenant à la multiplication de la fréquence par une certaine valeur. Si l’axe gradué mesure 20cm, on peut représenter les onze premiers B♭ (de B♭0 à B♭10) en les espaçant 2cm. Donc 2cm représentera une multiplication par 2 de la fréquence.

Le « zoom de B♭0 à B♭4 » prend maintenant la moitié de l’axe ! Et c’est justement sur cette moitié que l’on va pouvoir observer la progression des harmoniques.

fondam.      f ≈  30   n = 22   B♭0
harmo  1    2f ≈  60   n = 34   B♭1   oct
harmo  2    3f ≈  90   n = 41   F 2   5te
harmo  3    4f ≈ 120   n = 46   B♭2
harmo  4    5f ≈ 150   n = 50   D 3   3ce M
harmo  5    6f ≈ 180   n = 53   F 3
harmo  6    7f ≈ 210   n = 56   A♭3   ♭7
harmo  7    8f ≈ 240   n = 58   B♭3
harmo  8    9f ≈ 270   n = 60   C 4   2
harmo  9   10f ≈ 300   n = 62   D 4
harmo 10   11f ≈ 330   n = 64   E 4   ♯4
harmo 11   12f ≈ 360   n = 65   F 4
harmo 12   13f ≈ 390   n = 66   G♭4   ♭6
harmo 13   14f ≈ 420   n = 68   A♭4
harmo 14   15f ≈ 450   n = 69   A 4   7
harmo 15   16f ≈ 480   n = 70   B♭4

Visualisation avec des petits marqueurs sur les notes de la gamme majeure de C, en supposant que C est la fondamentale.

0-----------1------2----3---4--5--6-7-8-9-012-345
C D EF G A BC D EF G A BC D EF G A BC D EF G A BC

Reste à expliquer pourquoi il y a un trou au niveau de la 6 naturelle…

Différents cercles

Le cercle chromatique

(source)

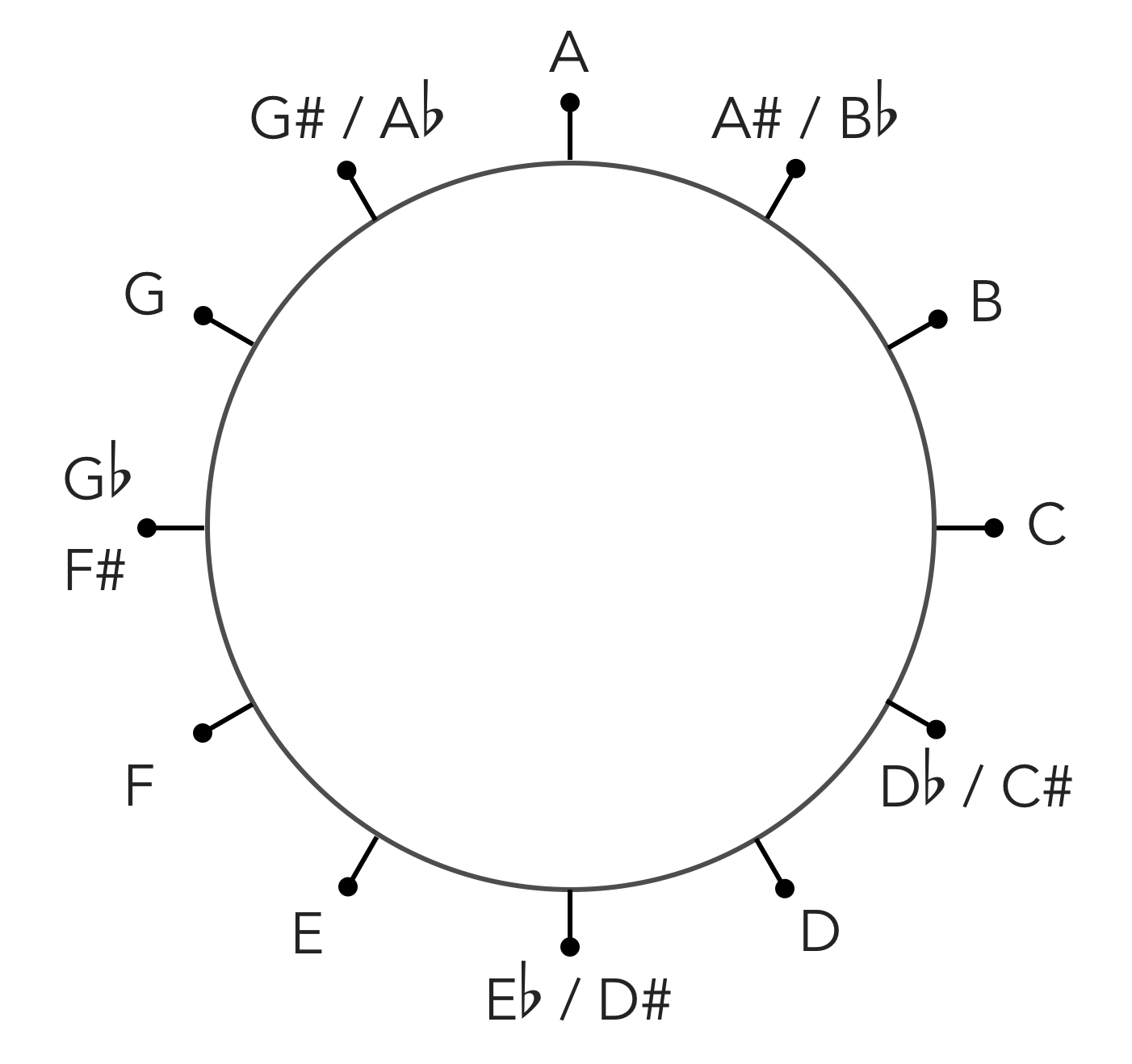
Le cercle des noms de notes

(source)

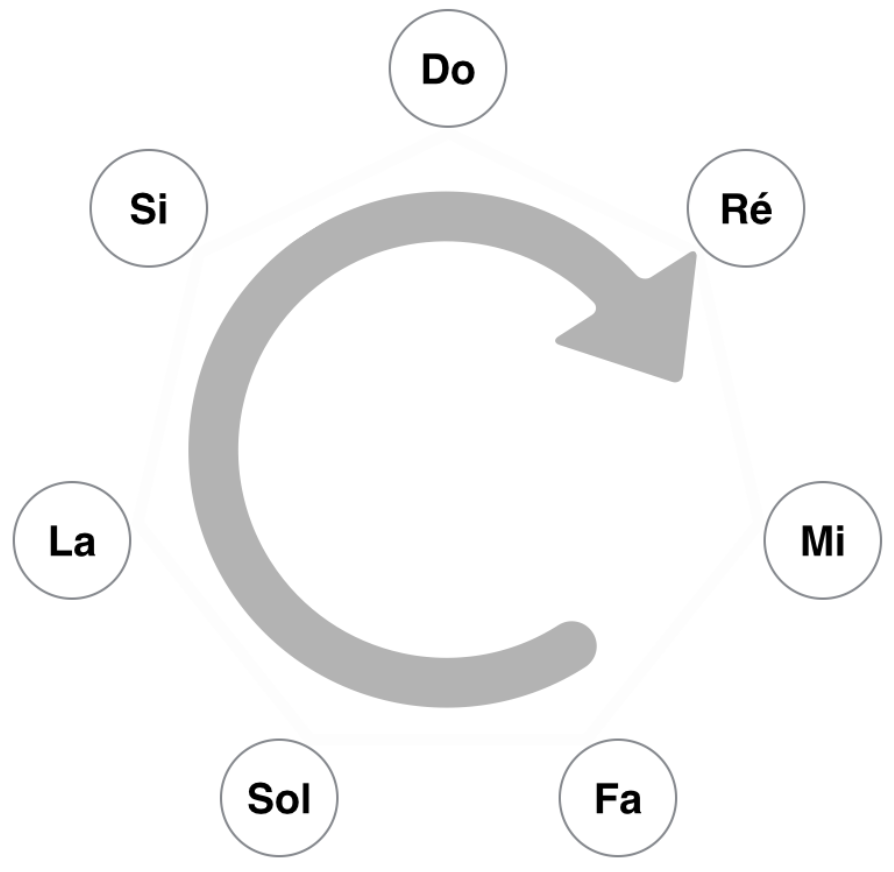
Les cercles diatoniques

Sur le modèle du cercle précédent, on pourrait, en respectant les intervalles 2212221, construire toutes les autres gammes majeures.

Le cercle (ou cycle) des quintes

Sur ce cercle, un cran dans le sens des aiguilles d’une montre correspond à « monter de 7 demi-tons ». Pourquoi le cycle « des quintes » ? La réponse plus bas.

Deux façons de voir ce cercle :

1. on enroule cette droite :

… E♭♭ B♭♭ F♭ C♭ G♭ D♭ A♭ E♭ B♭ F C G D A E B F♯ C♯ G♯ D♯ A♯ E♯ B♯ Fx Cx …

2. on se déplace dans le cercle chromatique :

On obtient ceci :

Auquel nous ajouterons plus tard le concept d’accords.

Différents types de sauts

Sur le cercle chromatique (voir ci-dessus), on compte le nombre de sauts en demi-tons. Il y a par exemple un demi-ton entre C et C♯.

Sur un cercle diatonique (voir ci-dessus), on numérote la note cible en comptant à partir de 1. Par exemple D est la seconde de C dans la gamme de C majeur.

Harmonisation à trois sons de la gamme majeure

Exemple avec la gamme majeure de Do

Une façon simple pour construire des accords : « empiler » des tierces. Les nombres séparant les notes sont les écarts chromatiques en demi-tons.

Do  2  Ré  2  Mi  1  Fa  2  Sol  2 La  2  Si  1  Do  2  Ré  2  Mi  1  Fa
Do      4     Mi      3     Sol                                            I M
       Ré      3     Fa      4     La                                     II m
              Mi      3     Sol     4     Si                             III m
                     Fa      4     La      3     Do                       IV M
                            Sol     4     Si      3     Ré                 V M
                                   La      3     Do      4                VI m
                                          Si      3     Ré      3    Fa  VII o
 

Les accords sont de type 43, 34, ou 33, les musiciens disent respectivement « majeur », « mineur » ou « diminué ».